Heidi Howard博士论文原作：论文原著-英文版
Flexible Paxos 大本营：Flexible Paxos 博客官网
Heidi Howard 在 Dockercon 2017上的演讲：使用灵活的Paxos构建可扩展、弹性和一致的系统
Heidi Howard 博士于2016年在伦敦 OSCON 的演讲幻灯片：分布式共识：使不可能成为可能-分布式共识领域的关键结果概述
由于市面上关于 Flexible Paxos 的文章较少，也没有见到 Flexible Paxos 算法论文的中译版，所以本篇文章打算对论文做一个简单的翻译。若有不准确的地方恳请留言斧正。

Flexible Paxos：重新审视法定人数交集

Author：海蒂·霍华德(1,2) 达丽娅·马尔基(1) 亚历山大·斯皮格曼(1,3)
Date：2016 年 8 月 25 日，星期四

剑桥大学计算实验室，英国剑桥，heidi.howard@cl.cam.ac.uk

VMware Research，美国帕洛阿尔托，dahliamalkhi@gmail.com

维特比电气工程系，海法理工学院，32000，以色列，sashas@tx.technion.ac.il

Abstract

分布式共识是现代分布式系统不可或缺的一部分。广泛采用的 Paxos 算法使用两个阶段，每个阶段都需要多数同意才能可靠地达成共识。在本文中，我们证明作为许多生产系统基础的 Paxos 是保守的。具体来说，我们观察到 Paxos 的每个阶段都可能使用非相交的群体。多数法定人数不是必需的，因为仅需要跨阶段交叉。
利用这种对原始公式中的要求的弱化，我们提出了Flexible Paxos，它概括了Paxos算法以提供灵活的仲裁。我们证明了Flexible Paxos在现有的分布式系统中是安全、高效且易于使用的。最后，我们讨论了这一结果的广泛影响。例如，当接受器数量为偶数时，通过将第二阶段仲裁的大小减少 1 来提高可用性，并利用小的不相交的第二阶段仲裁来加速稳态。

Introduction

分布式共识是面对失败时仍能达成一致的问题。这是现代分布式系统中的一个常见问题，其应用范围从分布式锁定和原子广播到强一致的键值存储和状态机复制[35]。 Lamport 的 Paxos 算法 [18, 19] 就是这个问题的解决方案之一，自其发布以来，它已被广泛应用于教学、研究和实践。
Paxos 的核心是使用两个阶段，每个阶段都需要一部分参与者（称为法定人数）同意才能继续。 Paxos的安全性和活跃性是建立在保证任意两个法定人数相交的基础上的。
为了满足这一要求，法定人数通常由固定参与者组中的任何多数组成，尽管也提出了其他法定人数方案。
在实践中，我们通常希望就一系列值达成一致，称为 Multi-Paxos [19]。我们使用Paxos的第一阶段建立一个参与者作为领导者，并使用Paxos的第二阶段提出一系列 value。要承诺某个值，领导者必须始终与至少法定人数的参与者进行沟通，并等待他们接受该值。
在本文中，我们弱化了原始协议中所有法定人数相交的要求，仅要求来自不同阶段的法定人数相交。在 Paxos 的每个阶段中，使用不相交仲裁是安全的，并且多数仲裁不是必需的。我们将这种新的表述称为Flexible Paxos (FPaxos)，因为它允许开发人员灵活地为两个阶段选择法定人数，前提是他们满足上述要求。严格来说，FPaxos 比 Paxos 更通用，并且具有相交群体的 FPaxos 相当于 Paxos。
鉴于 Multi-Paxos 及其变体的广泛部署，这样的结果具有广泛的实际应用价值。由于 Paxos 的第二阶段（复制）比第一阶段（领导者选举）更常见，因此我们可以使用 FPaxos 来减少常用的第二阶段仲裁的大小。例如，在一个 10 个节点的系统中，我们可以安全地只允许 3 个节点参与复制，前提是在从领导者故障中恢复时需要 8 个节点参与。这种以增加第 1 阶段法定人数为代价减少第 2 阶段法定人数的策略在本文正文中被称为简单法定人数。
简单的仲裁系统减少了延迟，因为领导者将不再需要等待大多数参与者接受提案。同样，它提高了稳态吞吐量，因为不相交的参与者集现在可以接受提案，从而更好地利用参与者并减少网络负载。我们为此付出的代价是可用性降低，因为系统可以容忍更少的故障，同时从领导者故障中恢复。
稍后，我们将令人惊讶地说明，并不总是需要为了稳定状态性能而牺牲可用性。示例包括当接受器数量为偶数时将第二阶段法定人数的大小减少一，以及利用诸如网格法定人数之类的法定人数系统来减少两个阶段的法定人数大小。
在下一节中，我们使用标准术语概述基本 Paxos 算法。已经熟悉该算法的读者应该直接进入下一节。在第 3 节中，我们详细描述了观察结果，然后在第 4 节中阐述了为什么这种灵活性在实践中有用。 §5 非正式地描述了为什么削弱 Paxos 对群体交集的假设是安全的。在第 6 节中，我们评估了 FPaxos 的简单实现并证明了其有用性。第 7 节概述了如何动态选择法定人数，第 8 节将 FPaxos 与该领域的现有工作联系起来。附录包括 FPaxos 算法的 TLA+ [20] 规范，该算法已根据我们的安全假设进行了模型检查。

Paxos

我们希望在一组进程之间决定一个值 v。系统是异步的，每个进程都可能失败，并且它们之间传递的消息可能会丢失。每个进程都有一个或多个角色。我们有三个角色：提议者，一个希望选择特定值的过程；接受者，一个同意并坚持决定值的过程；或者学习者，一个希望学习决定值的过程。
拥有候选值的提议者将尝试向接受者提议该值。如果已经选择了一个值，提议者将学习它。提议值的过程有两个阶段：阶段 1 和阶段 2，每个阶段都需要大多数接受者同意才能继续。我们现在将详细了解每个阶段：
第一阶段 - 准备和承诺
i 提议者选择一个唯一的提议编号 p 并向接受者发送prepare(p)。
ii 每个接受者接收prepare(p)。如果 p 是承诺的最高提案编号，则 p 被写入持久存储，并且接受者回复 Promise(p’,v’)。 (p’,v’) 是最后接受的提案（如果存在），其中 p’ 是提案编号，v’ 是相应的提案值。
iii 一旦提议者收到大多数接受者的承诺，就会进入第二阶段。否则，它可能会使用更高的提案编号重试。

第 2 阶段 - 提议并接受
i 提案者现在必须选择一个值 v。如果在第 1 阶段返回了多个提案，则它必须选择与最高提案编号相关的值。如果没有返回提案，则提案者可以选择自己的 v 值。然后提案者将 suggest(p,v) 发送给接受者。
ii 每个接受者收到一个提议(p,v)。如果p等于或大于最高承诺提案编号，则将承诺提案编号和接受的提案写入持久存储，接受者回复accept(p)。
iii 一旦提议者收到大多数接受者的accept(p)，它就知道v值已经决定了。否则，它可能会使用更高的提案编号再次尝试阶段 1。
Paxos 保证一旦决定了一个值，这个决定就是最终的，并且
不能选择不同的值。如果 n 个接受者中的 ⌊n/2⌋ + 1 个接受者已启动并能够通信，Paxos 将达成协议。证明进展需要我们对系统的同步性做出一些假设，因为我们不能保证真正的异步系统的进展[7]。

图 1：不同系统规模下 LibPaxos3 的性能。实验设置的详细信息在§6 中给出。
通常，我们希望就一系列值达成一致，我们将其称为槽。我们可以使用不同的 Paxos 实例来决定序列中的每个值，即第 i 个槽由第 i 个 Paxos 实例决定。然而在实践中，我们可以做得更好，这被称为 Multi-Paxos。
Paxos 的第一阶段与为任何给定实例提议的值无关，因此可以在知道要提议的值之前执行第一阶段。此外，我们可以将第一阶段聚合到一系列槽上。我们将完成第一阶段的提议者称为领导者。为了避免失一般性，我们引入另一个代理人，即客户，他是提案价值的起源。客户端可能位于系统外部，也可能与其他流程（例如提议者）位于同一地点。
图 1 说明了 Multi-Paxos 在实践中的执行情况。 x 轴显示系统中副本的数量，每个副本扮演提议者、接受者和学习者的角色。蓝线表示客户端观察到的提交延迟，红线表示平均请求吞吐量。正如我们所期望的，增加副本数量将增加延迟并降低吞吐量。这些发现与之前的研究一致 [29, 26]。
法定人数系统是我们选择哪些接受者集合能够形成有效法定人数的方法。据观察，Paxos 可以推广到用任何保证任意两个仲裁具有非空交集的仲裁系统来取代多数仲裁 [19, 21]。群体交集的基本定理指出，其弹性与参与者的负载（因此吞吐量）成反比[31]。因此，对于 Paxos 及其相交的群体，我们只能希望通过降低弹性来增加吞吐量，反之亦然。在本文的其余部分中，我们表明，通过削弱法定人数交叉要求，我们可以摆脱弹性和性能之间固有的权衡。

FPaxos

在本节中，我们观察到 Paxos 的通常描述（如第 2 节中给出）比必要的更加保守。为了解释这一观察结果，我们将区分 Paxos 第一阶段使用的法定人数（我们将其称为 Q1）和第二阶段使用的法定人数（称为 Q2）。
Paxos 对 Q1 和 Q2 都使用接受者的多数法定人数。通过要求法定人数至少包含大多数接受者，我们可以保证任何两个法定人数之间至少有一个共同的接受者。 Paxos 的安全性和进度证明是建立在所有法定人数相交的假设之上的。
我们观察到，仅需要第 1 阶段群体 (Q1) 和第 2 阶段群体 (Q2) 相交。不需要要求 Q1 彼此相交，也不需要 Q2 彼此相交。我们将其称为灵活 Paxos (FPaxos)，它概括了 Paxos 算法。如果我们允许任意一组至少 ⌊n/2⌋ + 1 个接受者在 FPaxos 中形成 Q1 或 Q2 群体，那么 FPaxos 就相当于 Paxos。
利用这一观察，我们可以利用许多非相交的群体系统。在其最直接的应用中，我们可以简单地减小 Q2 的大小，但代价是增加 Q1 仲裁的大小。
正如我们之前讨论的，Paxos 的第二阶段（复制）比 Multi-Paxos 中的第一阶段（领导者选举）更加频繁。因此，减少 Q2 的大小可以通过减少参与复制所需的接受器数量来减少常见情况下的延迟，提高系统对慢速接受器的容忍度，并允许我们使用不相交的接受器集来获得更高的吞吐量。我们为此付出的代价是，当我们需要建立新的领导者时，需要更多的接受者参与。虽然在稳定的系统中选举新的领导者是罕见的事件，但如果发生足够多的故障，我们无法形成 Q1 法定人数，那么在一些接受者恢复之前我们无法取得进展。
与 Paxos 一样，只要至少有足够的接受者启动并能够进行通信以形成 Q1 和 Q2 法定人数，系统就能够取得进展。与 Paxos 不同的是，只要我们能够形成与该阶段相对应的法定人数，我们就能够在给定阶段内取得进展。更具体地说，如果发生了足够多的故障，使得提议者无法再形成 Q1 法定人数，但能够形成较小的 Q2 法定人数，则系统可以继续安全地取得进展，直到需要新的领导者为止。如果接受者在当前领导者发生故障之前恢复，那么系统不会因此而遭受可用性损失。

Implications

现在我们将考虑观察到仅在 Paxos 的两个阶段之间需要群体交叉的实际含义。数据库和数据复制领域已经存在大量关于仲裁系统的文献，现在可以更有效地应用于共识领域。有趣的示例系统包括加权投票[9]、层次结构[15]和摇摇欲坠的墙[34]。然而现在，我们将通过考虑三个简单的仲裁系统示例来说明 FPaxos 的实用性：(1)多数仲裁 (2)简单群体 (3)网格群体。

Majority quorums

目前，Paxos 要求当接受器数量 n 为偶数【 Lamport 观察到多数可以扩展到包括 n/2 大小的集合的恰好一半 [16] 】时，使用大小为 n/2 + 1 的群体。根据我们的观察，我们可以安全地将 Q2 的大小从 n/2+1 减少 1 到 n/2，并保持 Q1 不变。这样的更改实施起来很简单，通过减少参与复制所需的接受器数量，我们可以减少延迟并提高吞吐量。此外，我们还提高了系统的容错能力。与 Paxos 一样，如果最多发生 n/2 − 1 次失败，那么我们保证能够取得进展。然而，与 Paxos 不同的是，如果恰好有 n/2 个接受者失败并且领导者仍然存在，那么我们就能够继续取得进展并且不会遭受可用性损失。
图 2 显示了实践中具有多数法定人数的 FPaxos 的两个示例跟踪。由于系统由四个接受器组成，FPaxos 对 Q1 使用多数（3 个接受器），但对 Q2 仅需要两个接受器。在示例中，两个提案者希望提交相互冲突的提案。在图 2a 中，提议者 1 首先执行 FPaxos 并提交其值 a。随后，提议者二执行一轮 Paxos 并获悉该值。在图 2b 中，两个提议者都成功执行了 FPaxos 的第一阶段，并同时向不相交的接受者集提交了冲突的提议值。两个 Q2 都会与两个 Q1 相交，因此只有其中一个会成功。不成功的提议者可以使用更高的提议编号重试并学习所选值。。

Simple quorums

我们将使用术语“简单仲裁”来指代仲裁系统，其中任何接受者都能够参与仲裁，并且每个接受者的参与都被平等地计算。简单法定人数是多数法定人数的直接概括。 Paxos 要求所有法定人数相交，因此，正如我们之前讨论的，每个法定人数必须至少包含严格多数的接受者才能满足此要求。
相比之下，FPaxos 仅要求来自不同阶段的群体相交。因此，具有简单法定人数的 FPaxos 必须要求 |Q1| + |Q2| > N. 我们知道，在实践中，第二阶段比第一阶段更常见，因此我们允许 |Q2| < N/2 并相应增加 Q1 的大小。对于给定的 Q2 大小和接受器数量 N，那么我们第一阶段仲裁的最小大小是 |Q1| = N − |Q2| + 1. FPaxos 将始终能够处理最多 |Q2| − 1 次失败。然而，如果在 |Q2| 之间至 N − |Q2| 发生故障时，我们可以继续复制，直到需要新的领导者为止。

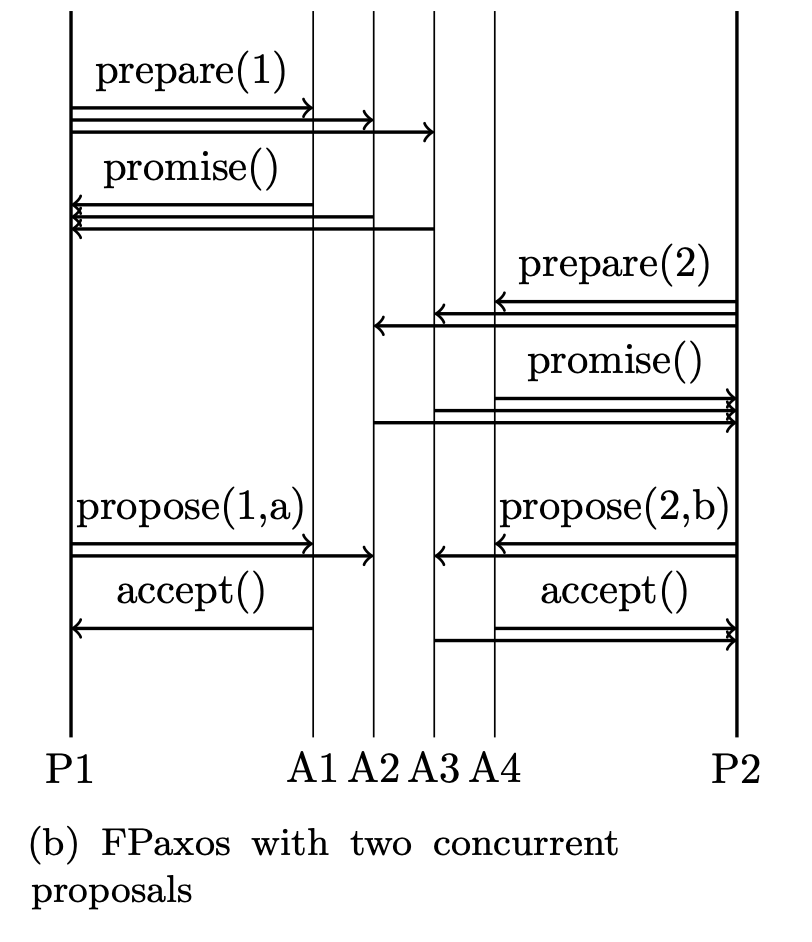
图 2：使用改进的多数仲裁的 FPaxos 执行示例。该系统由四个接受者（A1-A4）和两个提议者（P1，P2）组成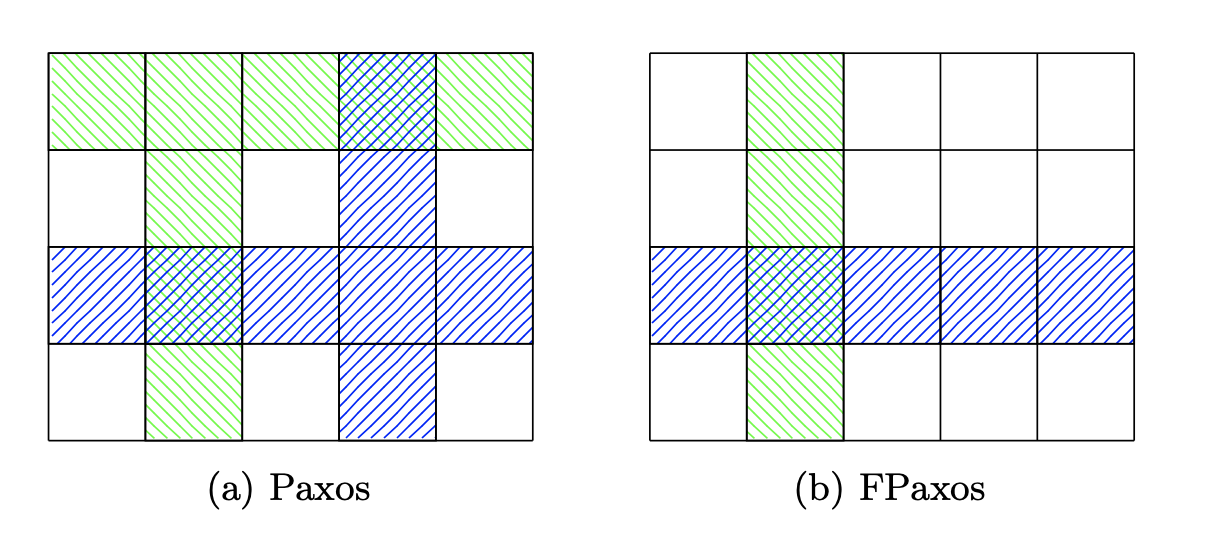

图 3：使用 5 x 4 网格形成 20 个接受器系统的法定人数的示例
正如之前所观察到的[25]，我们不需要向所有接受者发送准备和提议消息，只需至少向|Q1|发送即可。或|Q2| 接受者。如果这些接受者中的任何一个没有回复，那么领导者可以将消息发送给更多的接受者。这将消息数量从 4 × N 减少到 (2 × |Q1|) + (2 × |Q2|)。这是以增加延迟为代价的，因为领导者可能不会选择最快的接受者，并且在发生故障时必须重新传输。

Grid quorums

简单群体的关键限制是，减小 Q2 的大小需要相应增加 Q1 的大小才能继续确保交集。网格仲裁是替代仲裁系统的一个示例。网格仲裁可以通过在仲裁大小、选择仲裁时的灵活性和容错能力之间提供不同的权衡来减小 Q1 的大小。网格仲裁方案将 N 个节点排列成 N1 列乘 N2 行的矩阵，其中 N1 × N2 = N，仲裁由行和列组成。与许多其他仲裁系统一样，网格仲裁限制哪些接受器组合可以形成有效的仲裁。这一限制使我们能够减少法定人数的大小，同时仍然确保它们相交。
Paxos 要求所有 quorum 相交，因此一种合适的网格方案需要一行和一列来形成 quorum【实际上，使用一行加上其下方每一行中的一个网格项的任意选择就足够了。平均仲裁大小将变为 N1 + (1/2)N2，尽管最坏的情况仍然是 N1 +N2 −1】。图 3a 显示了使用此方案的 Q1 仲裁和 Q2 仲裁示例。这会将法定人数的大小从 N 的多数减少到 N1 + N2 − 1。可以容忍的故障数量范围为 MIN(N1,N2)，其中每行或每列中的一个节点失败到 (N1 − 1) × (N2 − 1)，只剩下一行和一列。
在 FPaxos 中，我们可以安全地将 Q1 的法定人数减少到大小为 N1 的一行，以及 Q2 的大小为 N2 的一列，示例如图 3b 所示。这种结构很有趣，因为来自同一阶段的法定人数永远不会相交，在实践中，对于在一组接受器之间均匀分配 FPaxos 的负载可能很有用。对于简单的仲裁，系统无法从领导者故障中恢复，同时任何一组|Q2| = N/2 接受者失败。现在有了网格法定人数，我们不再平等地对待所有失败，重要的是哪些接受者失败了，而不仅仅是有多少接受者失败了。回想一下，只要我们仍然可以形成该阶段的法定人数，我们就能够在给定阶段取得进展。例如，让我们考虑一下图 3 中任一网格中的四个接受器是否会失败。如果这些故障发生在两列中，那么两个系统都会取得进展。如果所有失败的节点都在一列内，那么 Paxos 将不会取得任何进展，但 FPaxos 将继续，直到需要新的领导者为止。同样，如果给定行中的所有节点都发生故障，FPaxos 将能够完成 Q1 并因此恢复所有过去的决策，然后它可以安全地退回到重新配置协议以删除或替换失败的接受器并继续取得进展。在实践中，故障不是独立的，因此我们可以将接受器分布在机器、机架甚至数据中心之间，以最大限度地减少同时发生故障的可能性。
通过思想实验，让我们考虑在使用网格法定人数时设置 N1 = 1 和 N2 = N 或等效地设置 |Q1| = N 和 |Q2| = 1，具有简单法定人数。任何单个接受者都足以形成 Q2，但是每个接受者都必须参与 Q1。在实践中，这将允许所有接受者在单跳中了解决定的值，但是在每个接受者都启动之前，我们将无法从领导者故障中恢复。
或者，让我们考虑在使用网格仲裁时设置 N1 = N 和 N2 = 1 或等效地设置 |Q1| = 1 和 |Q2| = N 具有简单法定人数。这将要求每个接受者都参与 Q2，但 Q1 只需要一个接受者。如果有任何接受者仍在运行，那么我们可以完成 Q1 并学习过去的决策。正如之前所观察到的 [25, 23]，这样的结构允许我们仅使用 f + 1 个接受器而不是 2f + 1 个接受器来容忍 f 次失败。

Safety

Lamport 的 Paxos 安全证明并未充分利用所做出的假设，即所有法定人数都会相交。为了完整起见，在本节中我们概述了 FPaxos 的安全性证明。
为了确保 FPaxos 的安全，做出的每个决定都必须是最终决定。换句话说，一旦决定了一个值，就不能决定不同的值。这可以正式表达为以下要求：

定理 1. 如果值 v 由提案编号 p 决定，v′ 由提案编号 p′ 决定，则 v = v′
对于要确定的给定值 v，必须首先提出它。因此，以下要求更加严格：

定理 2. 如果值 v 由提案编号 p 决定，则对于任何消息 suggest(p’,v’)，其中 p’ > p 则 v = v’
通过反证法证明，即假设v̸=v′。我们将考虑发送此类消息的最小提议编号 p’ > p。
令 Q1 和 Q2 分别为所有有效第 1 阶段和第 2 阶段法定人数的集合，A 为接受者集合。法定人数有效，前提是：

1
2
3

∀Q1 ∈Q1 :Q1 ⊆A (1) 					
∀Q2 ∈Q2 :Q2 ⊆A (2) 
∀Q1 ∈Q1,∀Q2 ∈Q2 :Q1 ∩Q2 ̸=∅ (3)

公式 1 指定每个可能的阶段 1 仲裁都是接受器的子集，与公式 2 类似。公式 3 指定由阶段 1 和阶段 2 仲裁组成的所有可能组合将在至少一个接受器中相交。
令 Qp,2 为提案编号 p 使用的第 2 阶段法定人数，Qp’,1 为提案编号 p’ 使用的第 1 阶段法定人数。令 A ̄ 为同时参与提案编号 p 使用的第 2 阶段仲裁和提案编号 p′ 使用的第 1 阶段仲裁的接受者集合，因此 A ̄ = Qp,2 ∩ Qp′,1。由于 Qp,2 ∈ Q2 且 Qp′,1 ∈ Q1，因此我们可以使用等式 3 来推断至少有一个接受者必须参与两个群体，A ̄ ̸= ∅。
让我们从一个接受者 acc 的角度来考虑事件的排序，其中 acc ∈ A ̄。他们要么先收到prepare(p’)，要么先收到propose(p,v)。我们将分别考虑以下每种情况：
情况1：
接受器 acc 在接收 suggest(p,v) 之前先接收prepare(p’)。当 acc 收到 propose(p,v) 时，其最后承诺的提案将为 p’ 或更高。当 p′ > p 时，它不会接受来自 p 的提议，然而，当 acc ∈ Qp,2 时，它必须接受提议(p,v)。这是一个矛盾，因此不可能是这样。
情况2：
接受器 acc 在接收prepare(p’)之前接收propose(p,v)。当acc接收到prepare(p’)时，有两种情况。任何一个：
情况 2a： 接受者 acc 最后承诺的提案已经高于 p’。那么它不会接受来自 p’ 的准备，但是由于 acc ∈ Qp’,1 它必须接受准备（p’）。这是一个矛盾，因此不可能是这样。
情况 2b： 接受者 acc 最后承诺的提案小于 p′，那么它将回复 Promise(q,v)，其中 p ≤ q < p′。在 p’ 的极小假设下，v 值将与 p 接受的值相同。
acc ∈ Qp′,1 因此promise(q,v)将至少是p′的提议者收到的响应之一。如果这是唯一接受的返回值，则将选择其值 v。 Qp’,1 成员还可能收到其他提案。回想一下 p < p′。对于收到的每个其他提案 (q′,v′′)，可以：
CASE (i) q′ < q：这些提案将被忽略，因为提案者必须选择与最高提案相关的值。
CASE (ii) p′ < q′：这种情况不会发生，因为接受者只有在最后承诺的值 < p′ 时才会回复prepare(p′)。

图 4：具有不同仲裁大小和 LibPaxos3 的 FPaxos 的吞吐量和平均延迟。
CASE (iii) p < q′ < p′ ：对于接受者来说，要接受 (q′, v′′)，那么它必须首先被提议。根据 p’ 的极小假设，这是不可能的。
因此，将选择值 v，这与发送 suggest(p’, v’) 的假设相矛盾。
我们在 TLA+ [20] 中提供了单值 FPaxos 协议的 2 页正式规范。我们使用不相交的法定人数对该规范进行了模型检查，并保留了要求 2。 FPaxos TLA+ 规范只是 [20] 中给出的 Paxos 规范的一个小修改。

Prototype

我们通过修改 LibPaxos3 【LibPaxos3源代码 https://bitbucket.org/sciascid/libpaxos】（一种常用的基准测试 Multi-Paxos 实现）来实现一个简单的 FPaxos。我们的修改只是概括了 Q1 和 Q2 的大小。简单的法定人数是随机选择的，消息仅发送到法定人数的节点。
LibPaxos3 是 C 语言的 Multi-Paxos 实现，它使用 TCP/IP 进行传输。对于每个实验，我们测试了 N 个副本，其中每个副本都是领导者、接受者和提议者。我们使用的请求大小为 64 字节，在任何给定时间都有 10 个正在进行的请求。我们的实验是在具有单核和 1GB RAM 的单个 Linux VM 中运行的，我们使用 mininet 【http://mininet.org】来模拟具有 20 ms 往返时间的 10 Mbps 网络。每个测试运行 120 秒，我们丢弃前 10 秒和最后 10 秒来测量系统在稳定状态下的情况。
图 4 显示了具有不同 Q2 仲裁大小的 Paxos 和 FPaxos 的稳态性能。这些结果正如我们所期望的：通过减少 Q2 仲裁的大小，我们发送更少的消息，从而提高吞吐量并减少延迟。
值得注意的是，这并不是完整的情况。首先，即使仲裁大小相同，FPaxos 的性能也优于普通 LibPaxos，因为 FPaxos 仅将消息发送到仲裁的副本，而 LibPaxos3 则将消息发送到所有副本。在实践中利用这种优化时，人们可能需要仔细权衡在实际设置中查找仲裁的策略，并考虑副本故障、相对副本速度和通信延迟。其次，与 Paxos 不同的是，当两个接受者失败时，Q2 大小为 2 的 FPaxos 将无法选举新的领导者。另一方面，在 8 个副本的系统中，Q2 大小为 4 的 FPaxos 比 Paxos 处理更多的故障，减少延迟
（从 42 毫秒到 37 毫秒）并提高吞吐量（从 198 请求/秒增加到 264 请求/秒）。这个原型证明了实现一个简单的 FPaxos 是微不足道的。我们证明，即使是非常简单的实现也能提高性能，并且我们相信为 FPaxos 设计的系统将获得更高的性能，
特别是通过利用不相交的接受器集和更智能的仲裁构建技术来提高容错能力。我们的原型源代码和相关材料可在线获取【https://github.com/fpaxos】。

Enhancements

我们观察到 FPaxos 的安全性仅依赖于给定 Q1 将与具有较低提案编号的所有 Q2 相交的假设。因此，如果提案者能够了解哪些 Q2 已使用较小的提案编号，我们可以进一步削弱法定人数要求。然后，我们只要求提议者的 Q1 与这些而不是所有可能的 Q2 相交。
为了利用这一点，我们可以通过领导者选择法定人数并宣布其选择的机制来增强 FPaxos。实现这一点的方法有很多，但为了安全起见，领导者公开其法定人数选择的机制必须仔细地融入领导者选举协议中。详细信息不属于本文的讨论范围。简而言之，它类似于 Paxos 重新配置，并通过采用 Vertical Paxos [23] 的原理来实现。
这种增强的影响可能是深远的。例如，在 N = 100f 个节点的系统中，领导者可能会首先宣布大小为 f + 1 的固定 Q2，并且所有更高的提案编号（和读者）将只需要与该 Q2 相交。这使我们能够容忍 N − f 次失败。同样，领导者可以选择一小组 Q2 并宣布所有这些，从而在第 2 阶段提供更大的灵活性，但代价是第 1 阶段的可用性较低。领导者还可以使用动态选择机制随着时间的推移更改其法定人数选择。
我们预计这些增强功能和其他增强功能可能会为未来的实际系统设计带来许多新的可能性。

富有洞察力的状态机复制 (SMR) 范式 [17, 36] 是许多可靠系统的基础，包括分布式系统领域的开创性工作，如 Viewstamped Replication [32] 和 Isis [3]。 Paxos 算法为许多架构为复制状态机的生产系统提供了算法解决方案。 SMR 必须解决一个核心要素，即协议，Dwork 等人[6] 在最小同步假设下解决，这是 Paxos [18] 中单位置协议协议（称为 Synod）的基础。在其发明后的几十年里，Paxos 算法得到了广泛的研究：它已经用更简单的术语进行了解释 [19, 39]，针对实际系统进行了优化 [4, 11, 13, 33]，并扩展到处理重新配置 [23] 和任意失败[5]。
人们提出了 Paxos 的许多变体。 Cheap Paxos [25] 固定单个阶段 2 法定人数，直到发生领导者替换。 Fast Paxos [21] 有一个无领导的快速路径协议，它利用大小为 f + [(f+1)/2] 的快速通道第 2 阶段群体。 Mencius [26]采用循环领导制度。 Ring-Paxos [28, 27] 将 Cheap Paxos [25] 中的思想应用于使用网络级多播的环覆盖。链复制[41]以菊花链（Daisy Chain）的方式连接接受器并将两个阶段合并为一个链扫描。 Generalized Paxos [22] 使用交换命令扩展了状态机复制，Egalarian Paxos [30] 使用大小为 f + [(f+1)/2] 的快速通道仲裁扩展了 Generalized Paxos。 EVE [14] 乐观地同时同意命令，并在不通勤的情况下解决冲突。 Corfu [2] 让领导者将其专属权力委托给任何提议者，以产生更好的并行性。还有许多其他变体； [40] 中给出了 Paxos 变体的综合分类。这些先前的工作建立在开创性协议 [32,3,6,18] 中提出的基础上，并专注于增强它们以实现更好的性能。我们的新观察重新审视了基础并对其进行了概括；它是完全正交的，可以集成到以前的协议以及实际的生产系统中，以进一步提高性能。
SMR 重新配置问题已在之前的几项工作中得到解决。有些使用共识命令来就下一个配置达成一致[32,24,23]，而另一些则使用第一阶段来确定第二阶段将使用哪个仲裁（从一组固定的仲裁中）[25,28]。 [23] 中出现了将稳态一致机制与重新配置事件分开的重新配置的通用框架。之前也研究过其他容错服务的重新配置，例如，在[10,1,12,38,8]中。正如第 7 节中所讨论的，可以采用这些工作中的想法来将 FPaxos 增强为可重构的动态系统。据我们所知，我们是第一个证明并实现 Paxos 泛化的人。在准备本出版物期间，Sougoumarane 独立地进行了与本工作相同的观察，并发布了一篇博客文章，为系统社区总结了它 [37]。

Conclusion

在本文中，我们描述了 FPaxos，它是广泛采用的 Paxos 算法的泛化，它不再要求来自同一 Paxos 相位的群体相交。我们相信这一结果会产生广泛的影响。
首先，在过去的二十年里，Multi-Paxos 得到了广泛的研究、部署和扩展。推广现有系统以使用 FPaxos 应该非常简单。向开发人员公开复制（第 2 阶段）仲裁大小将允许他们在容错和稳态延迟之间选择自己的权衡。
其次，通过不再要求复制仲裁相交，我们消除了可扩展性的重要限制。通过智能仲裁构建和务实的系统设计，我们相信新型可扩展、有弹性和高性能的共识算法现在是可能的。
致谢。我们要感谢以下人员的反馈：Jean Bacon、Jon Crowcroft、Stephen Dolan、Matthew Grosvenor、Anil Madhavapeddy、Sugu Sougoumarane 和 Igor Zabloctchi。

References

[1] Marcos K. Aguilera、Idit Keidar、Dahlia Malkhi 和 Alexander Shraer。没有共识的动态原子存储。 J. ACM，58(2):7:1–7:32，2011 年 4 月。URL：http://doi.acm.org/10.1145/1944345.1944348，doi：10.1145/1944345.1944348。
[2] Mahesh Balakrishnan、Dahlia Malkhi、John D. Davis、Vijayan Prabhakaran、Michael Wei 和 Ted Wobber。 Corfu：分布式共享日志。 ACM 翻译。计算。系统，31(4):10:1–10:24，2013 年 12 月。
[3] 肯·伯曼和托马斯·约瑟夫。在分布式系统中利用虚拟同步，第 21 卷。ACM，1987 年。
[4] 迈克·伯罗斯。用于松散耦合分布式系统的胖乎乎的锁服务。第七届操作系统设计与实现研讨会论文集，OSDI ’06，第 335-350 页，美国加利福尼亚州伯克利，2006 年。USENIX 协会。网址：http://dl.acm.org/itation.cfm?id=1298455.1298487。
[5] 米格尔·卡斯特罗和芭芭拉·利斯科夫。实用的拜占庭容错。在
第三届操作系统设计和实现研讨会论文集，OSDI ‘99，第 173-186 页，美国加利福尼亚州伯克利，1999 年。USENIX 协会。网址：http://dl.acm.org/itation.cfm?id=296806.296824。
[6] 辛西娅·德沃克、南希·林奇和拉里·斯托克迈尔。存在部分同步的情况下达成共识。美国计算机协会杂志 (JACM)，35(2)：288–323，1988 年。
[7] 迈克尔·J·费舍尔、南希·A·林奇和迈克尔·S·帕特森。不可能通过一个错误的流程达成分布式共识。美国计算机协会杂志 (JACM)，32(2)：374–382，1985 年。
[8] 伊莱·加夫尼和达丽娅·马尔基。通过简约的推测快照解决方案进行弹性配置维护。第 29 届国际分布式计算研讨会论文集，第 140-153 页。施普林格，2015。
[9] 大卫·K·吉福德。对复制数据进行加权投票。第七届 ACM 操作系统原理研讨会论文集，SOSP ’79，第 150–162 页，美国纽约州纽约市，1979 年。ACM。网址：http://doi.acm。 org/10.1145/800215.806583，doi：10.1145/800215.806583。
[10] 塞斯·吉尔伯特、南希·A·林奇和亚历山大·A·什瓦茨曼。 Rambo：用于动态网络的强大的、可重新配置的原子内存服务。分布式计算，23(4)：225–272，2010。
[11]帕特里克·亨特、马哈德夫·科纳尔、弗拉维奥·P·容奎拉和本杰明·里德。 Zookeeper：互联网规模系统的无等待协调。 2010 年 USENIX 会议记录，关于 USENIX 年度技术会议，USENIXATC’10，第 11-11 页，伯克利，加利福尼亚州，美国，2010 年。USENIX 协会。网址：http://dl.acm.org/itation.cfm?id=1855840.1855851。
[12] Leander Jehl、Roman Vitenberg 和 Hein Meling。 Smartmerge：原子存储重新配置的新方法。国际分布式计算研讨会，第 154-169 页。施普林格，2015。
[13] 弗拉维奥·P·朱奎拉、本杰明·C·里德和马可·塞拉菲尼。 Zab：用于主备份系统的高性能广播。可靠系统与网络 (DSN)，2011 年 IEEE/IFIP 第 41 届国际会议，第 245-256 页。 IEEE，2011。
[14] Manos Kapritsos、Yang Wang、Vivien Quema、Allen Clement、Lorenzo Alvisi 和 Mike Dahlin。关于 eve：多核服务器的执行验证复制。作为第 10 届 USENIX 操作系统设计和实现研讨会 (OSDI 12) 的一部分，第 237-250 页，2012 年。
[15]阿基尔·库马尔。分层仲裁共识：一种管理复制数据的新算法。 IEEE 传输。计算机，40(9):996–1004，1991 年 9 月。URL：http://dx.doi.org/10.1109/12.83661，doi:10.1109/12.83661。
[16]莱斯利·兰波特。可靠的分布式多进程系统的实现。计算机网络 (1976), 2(2):95 – 114, 1978。doi:http://dx.doi.org/10.1016/0376-5075(78)90045-4。
[17]莱斯利·兰波特。分布式系统中的时间、时钟和事件顺序。 ACM 通讯，21(7):558–565, 1978。
[18]莱斯利·兰波特。兼职议会。 ACM 翻译。计算。系统，16(2):133–169，1998 年 5 月。URL：http://doi.acm.org/10.1145/279227。 279229，doi：10.1145/279227.279229。
[19] 莱斯利·兰波特。 Paxos 变得简单。 ACM SIGACT 新闻（分布式计算专栏），2001 年。
[20]莱斯利·兰波特。指定系统：面向硬件和软件工程师的 TLA+ 语言和工具。 Addison-Wesley Longman Publishing Co., Inc.，美国马萨诸塞州波士顿，2002 年。
[21] 莱斯利·兰波特。快速 paxos。技术报告 MSR-TR-2005-112，微软研究院，2005 年。
[22] 莱斯利·兰波特。广义共识和 paxos。技术报告 MSR-TR-2005-33，微软研究院，2005 年 3 月。
[23] 莱斯利·兰波特、达丽娅·马尔基和周立东。垂直 paxos 和主备复制。第 28 届 ACM 分布式计算原理研讨会论文集，PODC ‘09，第 312-313 页，美国纽约州纽约市，2009 年。ACM。网址：http://doi.acm.org/10.1145/1582716。 1582783，doi：10.1145/1582716.1582783。
[24] 莱斯利·兰波特、达丽娅·马尔基和周立东。重新配置状态机。 ACM SIGACT 新闻，41(1):63–73，2010。
[25] 莱斯利·兰波特和迈克·马萨。便宜的paxos。 2004 年可靠系统和网络国际会议记录，DSN ’04，第 307 页，美国华盛顿特区，2004 年。IEEE 计算机协会。网址：http://dl.acm.org/itation.cfm?id=1009382.1009745。
[26] 毛燕华，Flavio P. Junqueira，和 Keith Marzullo。孟子：为广域网构建高效的复制状态机。第八届 USENIX 操作系统设计与实现会议论文集，OSDI’08，第 369–384 页，美国加利福尼亚州伯克利，2008 年。USENIX 协会。网址：http://dl.acm.org/itation.cfm?id=1855741.1855767。
[27] 帕里萨·贾利利·马兰迪、马可·普里米和费尔南多·佩多内。多环 paxos。 IEEE/IFIP 国际可靠系统和网络会议 (DSN 2012)，第 1-12 页。 IEEE，2012。
[28] Parisa Jalili Marandi、Marco Primi、Nicolas Schiper 和 Fernando Pedon。 Ring paxos：一种高吞吐量原子广播协议。 2010 年 IEEE/IFIP 国际可靠系统和网络会议 (DSN)，第 527-536 页。 IEEE，2010。
[29] P.J. Marandi、M. Primi、N. Schoper 和 F. Pedone。 Ring Paxos：一种高吞吐量原子广播协议。可靠系统和网络 (DSN)，2010 年 IEEE/IFIP 国际会议，第 527–536 页，2010 年 6 月。doi:10.1109/DSN.2010.5544272。
[30] 尤利安·莫拉鲁、大卫·G·安德森和迈克尔·卡明斯基。平等主义议会中有更多共识。第二十四届 ACM 操作系统原理研讨会论文集，SOSP ‘13，第 358–372 页，美国纽约州纽约市，2013 年。ACM。网址：http://doi.acm.org/10。 1145/2517349.2517350，doi：10.1145/2517349.2517350。
[31] 莫尼·纳尔和阿维沙伊·伍尔。仲裁系统的负载、容量和可用性。 SIAM J. Comput.，27(2):423–447，1998 年 4 月。URL：http://dx.doi.org/10.1137/S0097539795281232，doi:10.1137/S0097539795281232。
[32] 布莱恩·M·奥基 (Brian M Oki) 和芭芭拉·H·利斯科夫 (Barbara H Liskov)。 Viewstamped 复制：一种新的主复制方法，支持高可用性的分布式系统。第七届年度 ACM 分布式计算原理研讨会论文集，第 8-17 页。美国计算机学会，1988。
[33]迭戈·翁加罗和约翰·奥斯特豪特。寻找一种可理解的共识算法。在过程中。 USENIX 年度技术会议，第 305-320 页，2014 年。
[34] 大卫·法勒和阿维沙伊·伍尔。摇摇欲坠的墙：一类实用且高效的法定人数系统。第十四届年度 ACM 分布式计算原理研讨会论文集，PODC ‘95，第 120-129 页，美国纽约州纽约市，1995 年。ACM。网址：http://doi.acm.org/10。 1145/224964.224978，doi：10.1145/224964.224978。
[35] 弗雷德·B·施奈德。使用状态机方法实现容错服务：教程。 ACM 计算。 Surv.，22(4)：299–319，1990 年 12 月。URL：http://doi.acm.org/10.1145/98163.98167，doi：10.1145/98163.98167。
[36] 弗雷德·B·施奈德。使用状态机方法实现容错服务：教程。 ACM 计算调查 (CSUR)，22(4)：299–319，1990。
[37] 苏古·索古玛拉内。更灵活的paxos。 http://ssougou.blogspot。 com/2016/08/a-more-flexible-paxos.html。 [在线的; 2016 年 8 月 13 日访问]。
[38] 亚历山大·斯皮格曼、伊迪特·凯达尔和达丽娅·马尔基。动态重新配置：教程。 OPODIS 2015，2015。
[39] 罗伯特·范·雷内斯和德尼兹·阿尔廷布肯。 Paxos 变得中等复杂。 ACM 计算。 Surv.，47(3):42:1–42:36，2015 年 2 月。URL：http://doi.acm.org/10.1145/2673577，doi：10.1145/2673577。
[40] 罗伯特·范·雷内斯和德尼兹·阿尔廷布肯。 Paxos 变得中等复杂。 ACM 计算。 Surv.，47(3):42:1–42:36，2015 年 2 月。URL：http://doi.acm.org/10.1145/2673577，doi：10.1145/2673577。
[41] 罗伯特·范·雷内斯和弗雷德·B·施奈德。链式复制支持高吞吐量和可用性。 OSDI，第 4 卷，第 91-104 页，2004 年。